Presentation Summary: Rectangular Coordinate System, Pythagorean Theorem, Distance Formula, and Midpoint Formula. Advanced Algebra/Trigonometry Advanced. It is called 'Pythagoras' Theorem' and can be written in one short equation: a 2 + b 2 = c 2. Note: c is the longest side of the triangle; a and b are the other two sides; Definition. The longest side of the triangle is called the 'hypotenuse', so the formal definition is.
Pythagorean Theorem
by

Angie Head
This essay was inspired by a class that I am taking this quarter. Theclass is the History of Mathematics. In this class, we are learninghow to include the history of mathematics in teaching a mathematics. Oneway to include the history of mathematics in your classroom is to incorporateancient mathematics problems in your instruction. Another way is to introducea new topic with some history of the topic. Hopefully, this essay will giveyou some ideas of how to include the history of the Pythagorean Theoremin the teaching and learning of it.
We have been discussing different topics that were developed in ancientcivilizations. The Pythagorean Theorem is one of these topics. This theoremis one of the earliest know theorems to ancient civilizations. It was namedafter Pythagoras, a Greek mathematician and philosopher. The theorem bearshis name although we have evidence that the Babylonians knew this relationshipsome 1000 years earlier. Plimpton 322, a Babylonian mathematicaltablet dated back to 1900 B.C., contains a table of Pythagorean triples.The Chou-pei, an ancient Chinese text, also gives us evidence thatthe Chinese knew about the Pythagorean theorem many years before Pythagorasor one of his colleagues in the Pythagorean society discovered and provedit. This is the reason why the theorem is named after Pythagoras.
Pythagoras lived in the sixth or fifth century B.C. He founded the PythagoreanSchool in Crotona. This school was an academy for the study of mathematics,philosophy, and natural science. The Pythagorean School was more than aschool; it was 'a closely knit brotherhood with secret rites and observances'(Eves 75). Because of this, the school was destroyed by democratic forcesof Italy. Although the brotherhood was scattered, it continued to existfor two more centuries. Pythagoras and his colleagues are credited with manycontributions to mathematics.
The following is an investigation of how the Pythagorean theorem has beenproved over the years.
Pythagorean Theorem
The theorem states that:
'The square on the hypotenuse of a right triangle is equal to the sum of the squares on the two legs' (Eves 80-81).
This theorem is talking about the area of the squares that are built oneach side of the right triangle.
Accordingly, we obtain the following areas for the squares, where thegreen and blue squares are on the legs of the right triangle and the redsquare is on the hypotenuse.

area of the green square is
area of the blue square is
area of the red square is
From our theorem, we have the following relationship:
area of green square + area of blue square = area of red square or
As I stated earlier, this theorem was named after Pythagoras because hewas the first to prove it. He probably used a dissection type of proof similarto the following in proving this theorem.
'Let a, b, c denote the legs and the hypotenuse of the given righttriangle, and consider the two squares in the accompanying figure, eachhaving a+b as its side. The first square is dissected into six pieces-namely,the two squares on the legs and four right triangles congruent to the giventriangle. The second square is dissected into five pieces-namely, the squareon the hypotenuse and four right triangles congruent to the given triangle.By subtracting equals from equals, it now follows that the square on thehypotenuse is equal to the sum of the squares on the legs' (Eves 81).
Consider the following figure.
The area of the first square is given by (a+b)^2 or 4(1/2ab)+ a^2 + b^2.
The area of the second square is given by (a+b)^2 or 4(1/2ab) + c^2.
Since the squares have equal areas we can set them equal to another andsubtract equals. The case (a+b)^2=(a+b)^2 is not interesting. Let's do theother case.
4(1/2ab) + a^2 + b^2 = 4(1/2ab)+ c^2
Subtracting equals from both sides we have
concluding Pythagoras' proof.
Bhaskara's First Proof
Bhaskara's proof is also a dissection proof. It is similar to the proofprovided by Pythagoras. Bhaskara was born in India. He was one of the mostimportant Hindu mathematicians of the second century AD. He used the followingdiagrams in proving the Pythagorean Theorem.
In the above diagrams, the blue triangles are all congruent and the yellowsquares are congruent. First we need to find the area of the big squaretwo different ways. First let's find the area using the area formula fora square.
Thus, A=c^2.
Now, lets find the area by finding the area of each of the components andthen sum the areas.
Area of the blue triangles = 4(1/2)ab
Area of the yellow square = (b-a)^2
Area of the big square = 4(1/2)ab + (b-a)^2
= 2ab + b^2 - 2ab + a^2
= b^2 + a^2
Since, the square has the same area no matter how you find it
A = c^2 = a^2 + b^2,
concluding the proof.

Bhaskara's Second Proof of the Pythagorean Theorem
In this proof, Bhaskara began with a right triangle and then he drewan altitude on the hypotenuse. From here, he used the properties of similarityto prove the theorem.
Now prove that triangles ABC and CBE are similar.
It follows from the AA postulate that triangle ABC is similar to triangleCBE, since angle B is congruent to angle B and angle C is congruent to angleE. Thus, since internal ratios are equal s/a=a/c.
Multiplying both sides by ac we get
sc=a^2.
Now show that triangles ABC and ACE are similar.
As before, it follows from the AA postulate that these two triangles aresimilar. Angle A is congruent to angle A and angle C is congruent to angleE. Thus, r/b=b/c. Multiplying both sides by bc we get
rc=b^2.
Now when we add the two results we get
sc + rc = a^2 + b^2.
c(s+r) = a^2 + b^2
c^2 = a^2 + b^2,
concluding the proof of the Pythagorean Theorem.
The twentieth president of the United States gave the following proof tothe Pythagorean Theorem. He discovered this proof five years before he becomePresident. He hit upon this proof in 1876 during a mathematics discussionwith some of the members of Congress. It was later published in the NewEngland Journal of Education.. The proof depends on calculating thearea of a right trapezoid two different ways. The first way is by usingthe area formula of a trapezoid and the second is by summing up the areasof the three right triangles that can be constructed in the trapezoid. Heused the following trapezoid in developing his proof.
First, we need to find the area of the trapezoid by using the area formulaof the trapezoid.
A=(1/2)h(b1+b2) area of a trapezoid
In the above diagram, h=a+b, b1=a, and b2=b.
A=(1/2)(a+b)(a+b)
=(1/2)(a^2+2ab+b^2).
Now, let's find the area of the trapezoid by summing the area of the threeright triangles.
The area of the yellow triangle is
A=1/2(ba).
The area of the red triangle is
A=1/2(c^2).
The area of the blue triangle is
A= 1/2(ab).
The sum of the area of the triangles is
1/2(ba) + 1/2(c^2) + 1/2(ab) = 1/2(ba + c^2 + ab) = 1/2(2ab + c^2).
Since, this area is equal to the area of the trapezoid we have the followingrelation:
(1/2)(a^2 + 2ab + b^2) = (1/2)(2ab + c^2).
Multiplying both sides by 2 and subtracting 2ab from both sides we get
concluding the proof.
Pythagoras
Over 2000 years ago there was an amazing discovery about triangles:
When a triangle has a right angle (90°) ...
... and squares are made on each of the three sides, ...
... then the biggest square has the exact same area as the other two squares put together!
It is called 'Pythagoras' Theorem' and can be written in one short equation:
a2 + b2 = c2
Note:
- c is the longest side of the triangle
- a and b are the other two sides
Definition
The longest side of the triangle is called the 'hypotenuse', so the formal definition is:
In a right angled triangle:
the square of the hypotenuse is equal to
the sum of the squares of the other two sides.
Sure ... ?
Let's see if it really works using an example.
Example: A '3,4,5' triangle has a right angle in it.
Let's check if the areas are the same: 32 + 42 = 52 Calculating this becomes: 9 + 16 = 25 It works ... like Magic! |
Why Is This Useful?
If we know the lengths of two sides of a right angled triangle, we can find the length of the third side. (But remember it only works on right angled triangles!)
How Do I Use it?

Write it down as an equation:
Then we use algebra to find any missing value, as in these examples:
Example: Solve this triangle
You can also read about Squares and Square Roots to find out why √169 = 13
Example: Solve this triangle.
Example: What is the diagonal distance across a square of size 1?
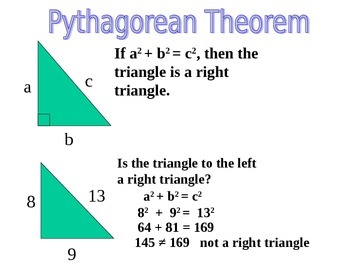
It works the other way around, too: when the three sides of a triangle make a2 + b2 = c2, then the triangle is right angled.
Example: Does this triangle have a Right Angle?
Does a2 + b2 = c2 ?
- a2 + b2 = 102 + 242 = 100 + 576 = 676
- c2 = 262 = 676
They are equal, so ...
Yes, it does have a Right Angle!
Example: Does an 8, 15, 16 triangle have a Right Angle?
Does 82 + 152 = 162 ?
- 82 + 152 = 64 + 225 = 289,
- but 162 = 256
So, NO, it does not have a Right Angle
Example: Does this triangle have a Right Angle?
Does a2 + b2 = c2 ?
Yes, it does!
So this is a right-angled triangle
And You Can Prove The Theorem Yourself !
Get paper pen and scissors, then using the following animation as a guide:
- Draw a right angled triangle on the paper, leaving plenty of space.
- Draw a square along the hypotenuse (the longest side)
- Draw the same sized square on the other side of the hypotenuse
- Draw lines as shown on the animation, like this:
- Cut out the shapes
- Arrange them so that you can prove that the big square has the same area as the two squares on the other sides
Pythagoras Theorem Presentation Examples
Another, Amazingly Simple, Proof
Here is one of the oldest proofs that the square on the long side has the same area as the other squares.
Watch the animation, and pay attention when the triangles start sliding around.
You may want to watch the animation a few times to understand what is happening.
The purple triangle is the important one.
| becomes |
We also have a proof by adding up the areas.
| Historical Note: while we call it Pythagoras' Theorem, it was also known by Indian, Greek, Chinese and Babylonian mathematicians well before he lived ! |
Pythagoras Theorem Presentation Calculator
Activity: A Walk in the Desert